Polinómio
Origem: Wikipédia, a enciclopédia livre.

Gráfico de um polinômio de grau 5
Em matemática, funções polinomiais, polinómios (português europeu) ou polinômios (português brasileiro) são uma classe importante de funções simples e infinitamente diferenciáveis. Devido à natureza da sua estrutura, os polinómios são muito simples de se avaliar e por consequência são usados extensivamente em análise numérica.
Determinar as raízes de polinómios, ou "resolver equações algébricas", é um dos problemas mais antigos da matemática. Alguns polinômios, tais como f(x) = x2 + 1, não possuem raízes dentro do conjunto dos números reais. Se, no entanto, o conjunto de candidatos possíveis for expandido ao conjunto dos números imaginários, ou seja, se se passar a tomar em conta o conjunto dos números complexos, então todo o polinómio (não-constante) possui pelo menos uma raiz (teorema fundamental da álgebra).
Existe uma diferença entre a aproximação de raízes e a determinação de fórmulas concretas que as definem. Fórmulas para a determinação de raízes de polinómios de grau até ao 4º são conhecidas desde o século XVI (ver equação quadrática, Gerolamo Cardano, Niccolo Fontana Tartaglia). Mas fórmulas para o 5º grau têm vindo a escapar aos investigadores já há algum tempo. Em 1824, Niels Henrik Abel provou que não pode haver uma fórmula geral (envolvendo apenas as operações aritméticas e radicais) para a determinação de raízes de polinómios de grau igual ou superior ao 5º em termos de coeficientes (ver teorema de Abel-Ruffini). Este resultado marcou o início da teoria de Galois, onde se aplica a um estudo detalhado das relações entre raízes de polinómios.
[editar] Definição (caso real)
Para a sucessão de termos  (ou
(ou  ) com
) com 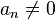 , um polinómio de grau n (ou também função racional inteira) é uma função que possui a forma
, um polinómio de grau n (ou também função racional inteira) é uma função que possui a forma

Alternativamente, o polinómio pode ser escrito recorrendo-se à notação sigma

Os números  são denominados de coeficientes do polinómio e o termo a0 de coeficiente constante, ou termo independente.
são denominados de coeficientes do polinómio e o termo a0 de coeficiente constante, ou termo independente.
Cada elemento somado avxv do polinómio é denomidado por termo. Um polinómio com um, dois ou três termos é chamado de monómio, binómio ou trinómio respectivamente.
Em relação ao grau, os polinómios podem ser classificados como a seguir:
- grau 0 - polinômio constante;
- grau 1 - função afim (polinômio linear, caso a0 = 0);
- grau 2 - polinômio quadrático;
- grau 3 - polinômio cúbico.
- ...
- grau n - polinômio de grau n.
Pode-se estender a definição de polinómio para incluir f(x) = 0, chamado polinômio nulo. O polinômio nulo não possui grau definido.
Uma equação polinômica obtem-se quando o polinômio é igualado a zero, ou seja:
 .
.
Desta forma podemos falar em raízes do polinômio f(x) e encontrar os valores de x que tornam a igualdade verdadeira, isto é, busca-se a raíz do polinômio f(x) que é um valor de x tal que torne f(x) = 0. Um número que satisfaz uma equação polinômica é chamado de número algébrico. Por exemplo:  é algébrico e valida o polinômio x2 − 2 = 0 pois
é algébrico e valida o polinômio x2 − 2 = 0 pois  .
.
[editar] Definição (genérica)
A definição acima de um polinómio com coeficientes reais (ou complexos) pode ser generalizada para polinómios com coeficientes em estruturas algébricas mais gerais. O resultado é o anel de polinômios.
Seja  um anel. Então podemos considerar o conjunto
um anel. Então podemos considerar o conjunto ![A[x]\,](http://upload.wikimedia.org/math/b/9/3/b93f85b3558cd23ebf9db9009a7d0f28.png) das funções
das funções  que tem suporte finito, ou seja, para as quais o conjunto
que tem suporte finito, ou seja, para as quais o conjunto  é finito. Essas funções representam os coeficientes do polinómio (notar que
é finito. Essas funções representam os coeficientes do polinómio (notar que  é uma forma de se escrever
é uma forma de se escrever  ).
).
O objetivo é escrever uma soma e um produto neste conjunto, de forma que as seqüências do tipo (k, 0, 0, ...) funcionem como os escalares, e a seqüência do tipo (0, 1, 0, ...) funcione como o x dos polinómios.
A definição de  e
e  é feita pelos seus coeficientes, ou seja:
é feita pelos seus coeficientes, ou seja:


Deve-se observar que as duas definições fazem sentido, pois a soma e o produto destas séries tem suporte finito.
Falta provar os axiomas de anel para ![(A[x], \otimes, \oplus)\,](http://upload.wikimedia.org/math/5/d/6/5d6947c6a5d3a4af387f3362750b2076.png) , o que é fácil mas trabalhoso, e que a função
, o que é fácil mas trabalhoso, e que a função
![\pi: A \to A[x]\,](http://upload.wikimedia.org/math/c/8/0/c806728c19029e9de0d9871e298ac64a.png)
definida por:

![]() 0\," src="http://upload.wikimedia.org/math/3/7/2/37250bb41227d6f1d4faafad685cab52.png">
0\," src="http://upload.wikimedia.org/math/3/7/2/37250bb41227d6f1d4faafad685cab52.png">
é um isomorfismo entre A e  .
.
Isso mostra que A pode ser visto como um sub-anel de ![A[x]\,](http://upload.wikimedia.org/math/b/9/3/b93f85b3558cd23ebf9db9009a7d0f28.png) .
.
Se o anel A possui identidade multiplicativa, então definindo x como a função:


![]() 1\," src="http://upload.wikimedia.org/math/f/7/8/f781a68a761bb3be28577197d474afe4.png">
1\," src="http://upload.wikimedia.org/math/f/7/8/f781a68a761bb3be28577197d474afe4.png">
verifica-se que os elementos de ![A[x]\,](http://upload.wikimedia.org/math/b/9/3/b93f85b3558cd23ebf9db9009a7d0f28.png) são todos da forma
são todos da forma  .
.
- Equações cujas soluções são números inteiros ou racionais são chamadas de Equações Diofantinas.
- Os polinómios até o grau n e o polinômio nulo formam um espaço vectorial que é normalmente denominado por Πn. Neste artigo os polinómios foram representados a partir de uma base monomial (ex.: 1,x,x2,...,xn) mas deve ser notado que qualquer outra sequência polinomial pode ser usada como base, como por exemplo os polinómios de Chebyshev.
- Se D é um domínio de integridade, então o anel dos polinómios
![D[x]\,](http://upload.wikimedia.org/math/a/8/6/a8647137662e2c0bad19813f6f524b7c.png) também é um domínio de integridade.
também é um domínio de integridade. - Se F é um corpo, então o anel dos polinómios
![F[x]\,](http://upload.wikimedia.org/math/0/3/2/032b23524fa379674779d192f5b84f66.png) é uma álgebra sobre o corpo F. Como espaço vectorial,
é uma álgebra sobre o corpo F. Como espaço vectorial, ![F[x]\,](http://upload.wikimedia.org/math/0/3/2/032b23524fa379674779d192f5b84f66.png) tem uma base enumerável. A base canónica é o conjunto
tem uma base enumerável. A base canónica é o conjunto  .
.
[editar] Tópicos de interesse









 (ou
(ou  ) com
) com 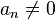 , um polinómio de grau n (ou também função racional inteira) é uma função que possui a forma
, um polinómio de grau n (ou também função racional inteira) é uma função que possui a forma

 são denominados de coeficientes do polinómio e o termo
são denominados de coeficientes do polinómio e o termo  .
. é algébrico e valida o polinômio
é algébrico e valida o polinômio  .
. um
um ![A[x]\,](http://upload.wikimedia.org/math/b/9/3/b93f85b3558cd23ebf9db9009a7d0f28.png) das
das  que tem
que tem  é finito. Essas funções representam os coeficientes do polinómio (notar que
é finito. Essas funções representam os coeficientes do polinómio (notar que  é uma forma de se escrever
é uma forma de se escrever  ).
). e
e  é feita pelos seus coeficientes, ou seja:
é feita pelos seus coeficientes, ou seja:

![(A[x], \otimes, \oplus)\,](http://upload.wikimedia.org/math/5/d/6/5d6947c6a5d3a4af387f3362750b2076.png) , o que é fácil mas trabalhoso, e que a
, o que é fácil mas trabalhoso, e que a ![\pi: A \to A[x]\,](http://upload.wikimedia.org/math/c/8/0/c806728c19029e9de0d9871e298ac64a.png)

 .
.

 .
.![D[x]\,](http://upload.wikimedia.org/math/a/8/6/a8647137662e2c0bad19813f6f524b7c.png) também é um domínio de integridade.
também é um domínio de integridade.![F[x]\,](http://upload.wikimedia.org/math/0/3/2/032b23524fa379674779d192f5b84f66.png) é uma
é uma  .
.







